
[운영체제/OS] 메모리 관리 - 페이징(Paging) 기법
kindof
·2021. 6. 14. 20:45
📖 0. 들어가면서
지난 포스팅에서 공부한 Partitioning, Buddy system 등의 메모리 관리 기법은 프로세스의 논리적인 메모리 주소를 물리적인 메인 메모리에 연속적인 Mapping을 전제했습니다.
[운영체제/OS] 메모리 관리 - 파티셔닝(Partitioning)과 버디 시스템(Buddy system)
이번 포스팅에서는 메모리 관리를 실전(?) 방법들에 대해서 공부하려고 합니다. 단, 지금부터 소개하는 방법들은 기본적으로 프로세스의 크기만큼 물리 메모리에 충분한 공간이 있음을 가정합
studyandwrite.tistory.com
하지만 지금부터 알아 볼 페이징(Paging) 기법은 물리적인 주소가 연속적이지 않은 상황에서도 매핑이 가능합니다. 어떤 방식인지 구체적으로 알아보도록 하겠습니다.
📒 1. Paging Concepts
1. frames: 물리 메모리(Physical Memory)를 일정한 사이즈로 분할한 블록
2. pages: 논리 메모리(Logical Memory)를 일정한 사이즈로 분할한 블록
프로세스의 논리적 주소 공간을 여러 개의 동일한 크기로 쪼갠 것을 페이지(Page)라고 하며, 물리적 주소 공간을 여러 개의 동일한 크기로 쪼갠 것을 프레임(Frame)이라고 합니다. 이 때 페이지와 프레임은 동일한 사이즈로 분할하도록 합니다.
그러면 논리적 주소의 한 부분은 (# of Page, Offset)으로 표현 가능하며, 물리적 주소의 한 부분은 (# of Frame, Offset)으로 표현할 수 있는데요.
이후에 페이징 기법은 이렇게 쪼개진 프레임과 페이지를 서로 매칭시킵니다. 아래 그림을 볼까요?

그림에서 왼쪽은 논리적 메모리 주소이며 오른쪽은 물리적 메모리 주소를 나타냅니다. 그림에서 볼 수 있듯, 두 개의 주소 공간은 일정한 크기의 페이지/프레임으로 쪼개져서 존재하며, 이 때 예를 들어 논리적 메모리의 특정 주소값은 "p1번째 페이지의 o1번째 Offset"이라는 식으로 표현 가능합니다. 마찬가지로 물리적 메모리의 특정 주소값은 "f2번째 프레임의 f2번째 Offset"이라는 식으로 표현 가능하죠.
💡 2. Virtual Address Translation
지금까지 살펴본 것처럼, 페이지는 논리적 주소 공간을 쪼갠 것이고, 프레임은 물리적 메모리 공간을 쪼갠 개념입니다. 그리고 페이지와 프레임은 각각 매핑이 되며, 이 때 반드시 연속적인 매핑을 전제로 하지 않습니다.
그러면 어떤 방식으로 페이지를 프레임에 매핑할까요? 아래 과정을 하나씩 이해해봅시다.
1) 기본적으로 모든 페이지는 각자가 매핑되는 프레임에 대한 정보가 기록된 페이지 테이블(Page table)을 갖습니다. 즉, 페이지 테이블은 페이지의 수만큼의 엔트리를 가집니다.
2) 논리적 메모리 주소는 (# of page, offset)으로 표현된다고 했고, 페이지의 크기와 프레임의 크기는 같다고 했죠?
3) 만약 시스템이 32KB(=1024*32byte)의 물리적 주소 공간을 갖고, 각 페이지는 1024byte의 공간을 갖는다고 해보겠습니다. 페이지와 프레임의 사이즈는 동일하므로 현재 물리적 주소 공간에 페이지는 총 32개(= 2^5개)가 존재합니다.
4) 이 때, 하나의 페이지 내에서 가질 수 있는 offset의 주소는 0부터 1023이 되고 프레임 역시 같은 사이즈니까 0부터 1023만큼의 offset이 존재합니다.
5) 그래서 Virtual address의 하위 10개 비트를 offset(0~1023)을 표시하는 데 사용하고, 총 프레임의 개수는 2^5개가 되니까 하위 5bit(5 LSB)를 매핑할 프레임 인덱스로 쓰면 됩니다.
5) 아래 그림처럼 4번째 page의 offset = 0인 블록은 0번째 frame의 offset = 0에 매핑이 되고, 3번째 page의 offset = 1023인 블록은 4번째 frame의 offset = 1023에 매핑됩니다.

offset 정보는(?) : 교수님께 여쭤보니 offset 정보는 그대로 복사된다고 합니다. 페이징 기법에서 중요한 개념은 각 페이지가 프레임에 어떻게 대응되느냐가 중요한 것이라고 합니다.
📋 3. Page Table Structure
프로세스 하나는 하나의 페이지 테이블을 가지고 있고, 테이블 안에는 프로세스의 모든 'Page To frame Mapping' 정보가 담겨있습니다.
하지만 페이지 테이블은 단순히 위와 같은 매핑 정보만 담고 있는 것이 아니고, Bit flags 정보를 담고 있는데요. Bit flag에는 Present bit, Dirty bit, Reference bit, Protection bit 등이 존재합니다.
예를 들어 Dirty bit는 해당 페이지가 수정된 적 있느냐, Reference bit은 해당 페이지가 참조된 적 있느냐, Present bit은 페이지 자체가 생성되어 있느냐 등의 정보를 담고 있죠.
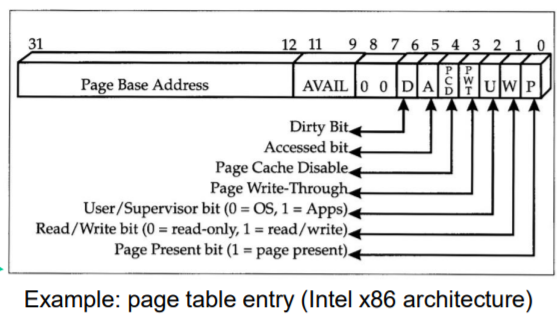
Dirty bit, Present bit, Reference bit은 나중에 다룰 페이지 교체 정책에서 "어떤 페이지를 evict할 것인가?", "물리 메모리에서 사용 중인가?"를 판단할 때 사용되기 때문에 중요한 녀석들입니다.
💀 4. Page Table Implementation Issue
지금까지 내용을 간단히 요약하면 페이지 테이블은 각 프로세스마다 존재하고, 각 페이지 테이블은 프로세스가 가지고 있는 페이지 수만큼의 엔트리를 가집니다. 그리고 각 엔트리는 매핑되는 프레임에 대한 정보와 Flag bit를 갖고 있습니다.
이렇게만 보면 별 문제가 없어보이지만, 사실 페이지 테이블을 구현하는 데는 크게 두 가지 이슈가 존재합니다.
✅ 1) Memory Access Overhead
사실 우리가 물리적 메모리에 저장된 정보를 읽기 위해서 두 번의 메모리 접근(Memory Access)을 하게 됩니다.
1) 페이지 테이블에 접근해서 매핑된 프레임의 정보를 읽어야 하고,
2) 실제 메모리에 접근해서 Data/Instruction을 읽어야 하기 때문이죠.
이 과정에서 필요한 두 번의 메모리 접근은 Memory Access Overhead를 발생시키게 됩니다.
이를 해결하기 위해 Associative Memory인 TLB(Translation Look-aside Buffer)를 이용하는데요. 일반 메모리는 주소에 접근해서 데이터를 반환하는 반면, Associative Memory는 인덱스를 이용해 그에 매칭되는 데이터를 저장해두고, 다음에 동일한 접근이 일어나면 해당 데이터를 빠르게 반환할 수 있게 합니다.
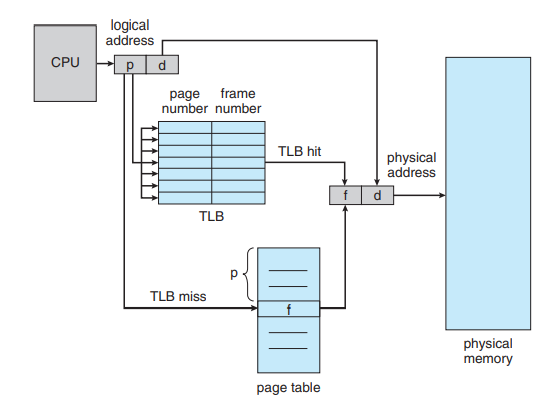
그런데 위처럼 TLB를 사용해서 프레임에 대한 매핑 정보를 빨리 알아보려고 했는데 TLB 테이블에 아직 프레임의 번호가 없으면 다시 페이지 테이블을 찾아가서 프레임 번호를 얻고, 이 녀석을 TLB에 저장해줘야 합니다. TLB의 크기는 정해져있기 때문에 모든 프레임 번호에 대한 데이터를 다 저장하고 있을 수 없기 때문이죠. 캐시와 동일한 개념이죠?
따라서, 이런 부분을 고려하기 위해서 Hit Ratio와 Effective Access Time(EAT) 라는 개념이 등장합니다.
Hit Ratio : Percentage of times that a page number is found in TLB
= r - Effective Access Time(EAT) = (1 + X) * r + (2 + X)(1 - r) = 2 + X - r
EAT에서 r은 Hit ratio를 의미하고 X는 아주 짧은 시간으로 TLB에 접근하는 시간을 의미합니다. EAT를 최소로 만드려면 r = 1로 만들어야 하는데 이는 Hit ratio = 1을 의미하고, TLB 테이블에 거의 모든 페이지와 프레임의 매핑 정보가 있다는 뜻이죠.
사실 이렇게 하면 EAT는 작아져서 효율은 좋아지지만 모든 내용이 TLB에 있으려면 Associative Register가 비싸기 때문에 비용적 문제가 생기는 한계가 존재합니다.
결국 여기서 이야기하고자 하는 바는 이런 식으로 TLB를 이용해서 CPU 메모리에 접근하는게 효율적인 메모리 접근 방법이라는 것입니다. 물론 여기에 드는 캐시의 크기와 비용 문제도 고려해야겠죠.
✅ 2) Handling Large Page Table
위에서 말한 것처럼 프로세스마다 1개의 페이지 테이블이 존재한다면, 메모리 이슈 문제가 생기게 됩니다.
예를 들어 2^32bit의 논리적 메모리가 존재하고 각 페이지 사이즈는 2^12bit, 페이지 테이블에서 하나의 엔트리의 크기는 4byte라고 해볼까요? 그러면 프로세스의 페이지 테이블은 약 2^20개의 페이지 엔트리를 들고 있어야 합니다.
페이지 엔트리의 개당 크기가 4bytes면 는 2^20 * 4bytes = 4Mbytes 정도가 되죠. 컴퓨터에서 돌아가는 프로세스의 수가 2^10개정도만 존재한다고 해도, 페이지 테이블의 용량만 4GB가 된다는 뜻입니다.
따라서 이렇게 큰 페이지 테이블들을 다 들고 다닐 수 없으므로 이를 해결할 수 있는 방법에 대한 고민이 필요하게 됩니다.
🔑 1) Multi-Level Paging
멀티 레벨 페이징은 논리적 주소 공간을 여러 개의 페이지 테이블 속에 나눠서 집어넣는 개념인데요. 예를 들어 1000페이지짜리 책이 있을 때 기존의 페이징 기법은 "38페이지의 열 번째 줄에 어떤 내용이 있다"는 식으로 페이지 테이블을 작성합니다.
반면, 두 단계 페이징을 적용하면 "해당 내용이 3번째 챕터의 5번째 페이지의 10번째 줄에 있다"는 식으로 알려줍니다. 챕터에 대한 테이블만 들고 다니고, 해당 챕터에 대한 테이블 안에 부분적인 페이지 테이블이 존재하는 것이죠.
멀티 레벨 페이징 기법은 모든 페이지 테이블을 들고 다니지 않아도 되기 때문에 메모리 이슈가 덜해지지만, Chapter -> page -> offset 순으로 접근을 해야하기 때문에 메모리 접근에 대한 오버헤드 이슈가 생기긴 합니다.

위에서 설명했던 것처럼, 32-bit Logical Address는 이제 20 bit의 페이지 번호를 나타내는 영역과 12 bit의 offset을 나타내는 영역으로 나뉘게 됩니다(그림에서 Outer Page의 p1은 42비트가 아니라 10비트로 수정해야 할 것 같습니다).
구체적으로 들여다보면, 20 bit 중에서 p1이 나타내는 10bit는 Outer page의 인덱스를 나타내고, p2은 Inner page의 인덱스를 나타냅니다. 다시 말해서, p1은 이제 하나의 프로세스가 가지는 페이지 테이블 전체를 지칭하게 되고, p2는 그 안에서 개별적으로 존재하는 페이지들을 가리키는 것이죠.
이렇게 되면, 모든 프로세스의 페이지 엔트리(약 4GB)를 들고 다니지 않고, 필요한 프로세스의 페이지만 불러다가 쓸 수 있게 됩니다.
🔑 2) Hased Page Table
이 방법은 32-bit 이상의 명령어 체제에서 주로 사용하는데 페이지 테이블에 페이지의 번호를 해시화(Hashing)해서 집어 넣는 방법입니다.
논리적 주소 공간의 페이지 번호 p를 해시한 결과값으로 해시 테이블을 검사하여 해당 물리적 메모리를 찾아가게 됩니다. 같은 해시 결과값에 대해서 리스트 하나를 이용할 수 있기 때문에 메모리 문제를 조금 해결할 수 있습니다.
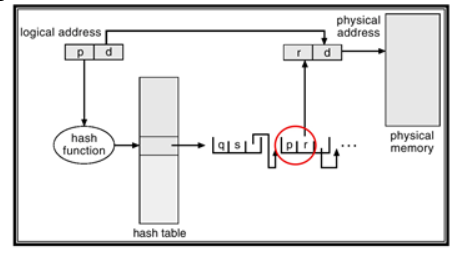
🔑 3) Inverted Page Table
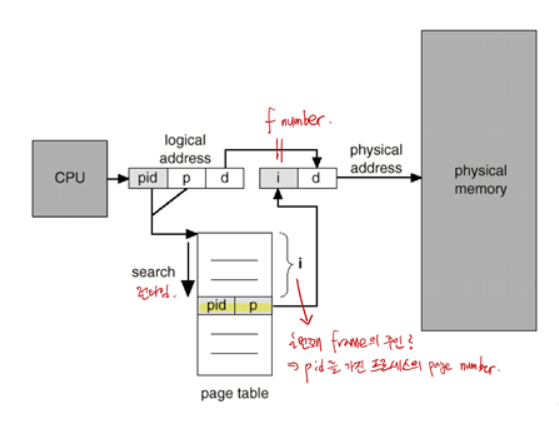
이전의 테이블들은 모두 논리적 주소 공간을 기준으로 한 테이블이었습니다. 프로세스 당 하나의 페이지 테이블을 갖고 있었고 나누어진 페이지의 순서대로 페이지 테이블에 순서대로 대응되는 구조였죠.
Inverted Page Table은 물리적 메모리 주소 입장에서 만들어진 테이블 구조입니다. 첫 번째 프레임은 테이블의 첫번째에 저장되고, 테이블의 각 프레임은 어떤 프로세스와 대응되는지에 대한 정보를 담습니다.
따라서 이전에는 테이블에 단순히 몇번째 프레임인지에 대한 정보만을 담고 있었다면, 이제는 프로세스 번호인 pid 값도 담고 있게 됩니다.
Inverted page table은 프로세스 당 하나의 페이지 테이블이 아니라 전체적인 하나의 테이블만 있으면 되는 장점이 있지만 테이블 크기가 커서 검색 시간이 좀 더 걸리는 단점이 있습니다.
또한 테이블에 pid와 page 정보가 없으면 원래 페이지 테이블에 가서 정보를 업데이트 하고...해야 되서 완벽한 전략은 아닙니다.
5. 나가면서
이번 시간에는 페이징 기법을 통한 메모리 관리에 대해 공부했는데요. 약간 복잡해보이지만, 논리적 주소 공간과 물리적 주소 공간을 동일한 크기의 블록으로 쪼개고 각 구간을 비연속적으로 매핑한다는 큰 개념으로 받아들이면 될 것 같습니다.
다음 포스팅에서는 세그멘테이션(Segmentation)을 통한 메모리 관리 기법에 대해 공부하고, 페이징 기법과 비교를 해보겠습니다.
'CS > OS' 카테고리의 다른 글
| [운영체제/OS] 메모리 관리 - 디맨드 페이징과 페이지 부재(Page Fault) Issue (0) | 2021.06.14 |
|---|---|
| [운영체제/OS] 메모리 관리 - 세그멘테이션(Segmentation)과 페이징 기법 (0) | 2021.06.14 |
| [운영체제/OS] 메모리 관리 - 파티셔닝과 버디 시스템(Buddy system) (0) | 2021.06.14 |
| [운영체제/OS] 메모리 관리 - 물리적, 논리적 주소 공간과 스와핑(Swapping) (0) | 2021.06.14 |
| [운영체제/OS] 데드락(Deadlock) 핸들링하기 (0) | 2021.06.14 |





