[Multicore] 효율적인 Matrix Multiplication

CS/Multicore & GPU

[Multicore] 효율적인 Matrix Multiplication - 멀티쓰레드와 캐시

kindof

2022. 4. 19. 17:13

0. Matrix Multiplication

아래는 N * N 크기의 행렬 A, B를 곱하여 그 결과인 N * N 행렬 C를 구하는 과정입니다.

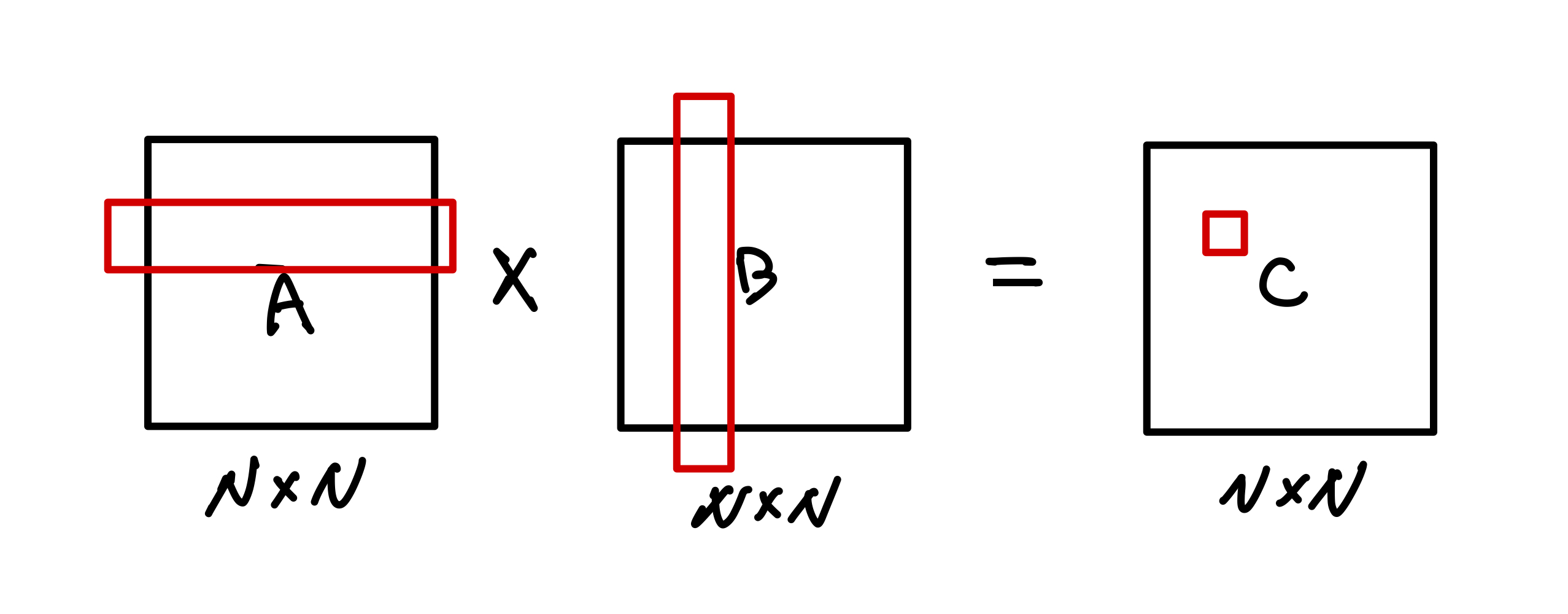
결과로 나오는 C 행렬의 (i, j)번째 값을 계산하기 위해서는 위 그림처럼 A 행렬의 i번째 행과 B행렬의 j번째 열의 원소들을 곱해야 합니다.

위 과정을 코드로 보면 아래와 같으며 두 개의 N * N 행렬의 곱셈에 드는 시간 복잡도는 O(N^3)임을 알 수 있습니다.

for i = 1 to n
    for j = 1 to n
    	for k = 1 to n
            C(i, j) = C(i, j) + A(i, k) * B(k, j)

자, 그러면 위 연산을 어떻게 멀티쓰레딩을 통해 병렬로 처리할 수 있을까요? 앞으로 몇 가지 방법에 대해 소개를 할텐데, 각 방법이 동작하는 방식과 특징에 대해 이해를 해보는 것이 중요합니다.

1. Column-wise Block Striping

Serial Implementation을 Parallel Implementation으로 구현할 때 처음 생각해봐야 하는 것은 어떤 기준으로 각 쓰레드에게 연산을 할당할 것인가입니다.

첫번째 방법으로 아래 그림과 같이 결과값 행렬 C의 각 Column에 대한 연산을 각 쓰레드에게 할당하여 처리하도록 해보겠습니다.

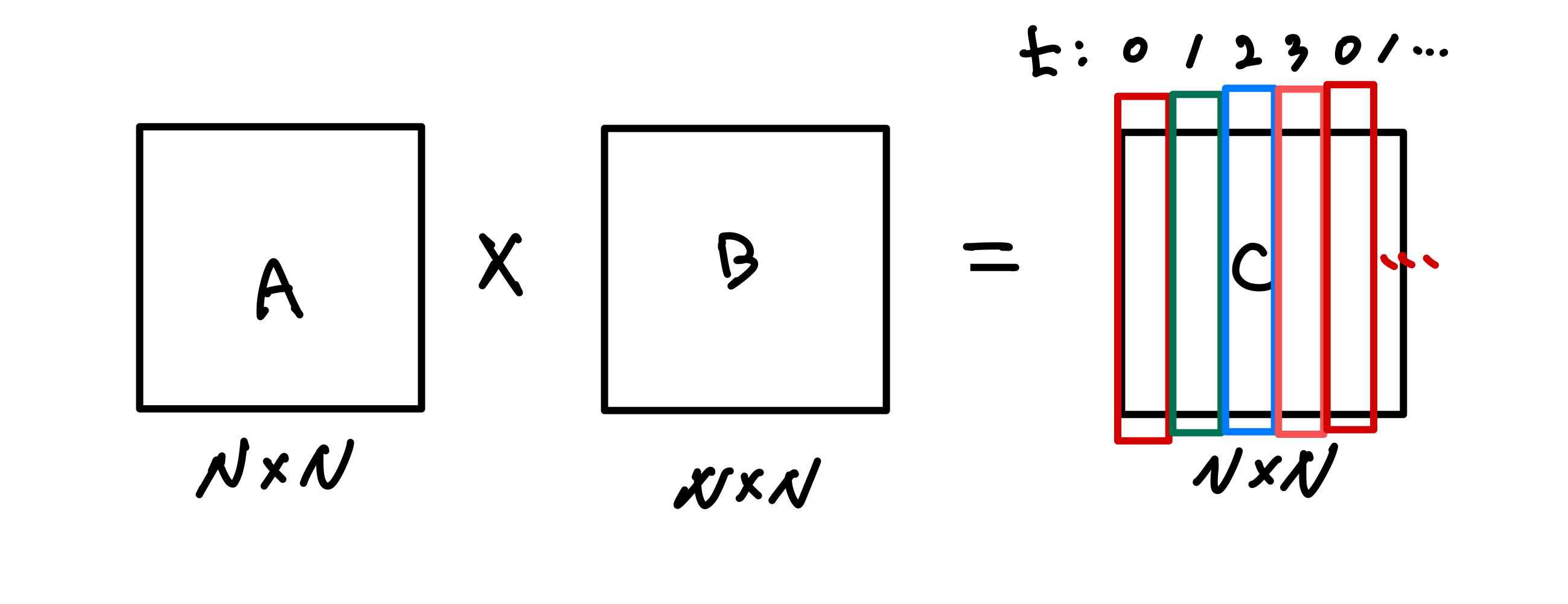
for i = 1 to n
    for j = tid to n step p    // Column block striping
        for k = 1 to n
        	C(i, j) = C(i, j) + A(i, k) * B(k, j)

위 코드에서 tid는 현재 쓰레드의 id를 의미하며, p는 전체 쓰레드의 개수를 의미합니다.

예를 들어 N = 10이고 p = 4라면, 0번째 쓰레드는 0, 4, 8번째 column을 처리하고, 1번째 쓰레드는 1, 5, 9번째 column, 2번째 쓰레드는 2, 6, 10번째 column, 3번째 쓰레드는 3번째 column을 처리하는 것이죠.

위와 같이 Column에 대해 block striping 방식으로 병렬 처리를 하게 되면 전체 시간복잡도는 O(N^3 / p)가 됩니다. 전체 작업을 p개의 쓰레드가 나누어서 처리하기 때문이죠.

1-1. False Sharing

하지만 위 방식은 False Sharing이라는 문제를 안고 있습니다. False sharing이란 CPU 내부의 코어와 코어간의 메모리 정보가 공유되어 하드웨어 적으로 병목현상이 일어나는 것을 뜻합니다. 보다 쉽게 말하면, 여러 개의 쓰레드가 공유하는 Cache line의 정보는 항상 Synchronous 해야 하며, 이에 따른 동기화가 필요할 때 병목 현상이 발생할 수 있다는 것인데요.

무슨 말인지 아래 그림을 통해 좀 더 구체적으로 이해해보겠습니다. 위 그림에서 각 쓰레드가 행렬 C를 읽어올 때 아래와 같이 Cache line의 일부분을 읽어오는 순간이 있을 겁니다. * 각 쓰레드는 반복해서 C에 데이터를 Write하기 때문에 Cache를 사용합니다.

이 상황에서 쓰레드 t0는 a 값을 연산하고, 쓰레드 t1은 b값을, 쓰레드 t2는 c값을 연산할텐데요. 그러면 세 개의 쓰레드 t0, t1, t2 관점에서는 동일한 Cache line에서 읽어왔는데 연산을 하고 보니, 세 녀석이 공유하는 Cache line의 데이터가 달라져버리게 된 것입니다. 그래서 각 쓰레드는 연산을 하고 난 뒤 기존에 읽어왔던 Cache line의 데이터와 달라진 점이 있는지 확인하고, 동기화를 시켜주는 작업이 더 필요해지는 것입니다.

결국, 이러한 False sharing으로 인해 위에서 언급했던 O(N^3 / p)라는 시간복잡도는 달성되지 못하게 됩니다.

2. Row-wise Block Striping

Row-wise Block Striping 방식은 False sharing을 피하기 위한 방법입니다. 아래와 같이 각 쓰레드에게 결과 행렬 C의 각 Row에 대한 연산을 맡김으로써 각 쓰레드가 Cache line을 읽어올 때 서로 공유되는 부분이 없도록 만드는 것이죠.

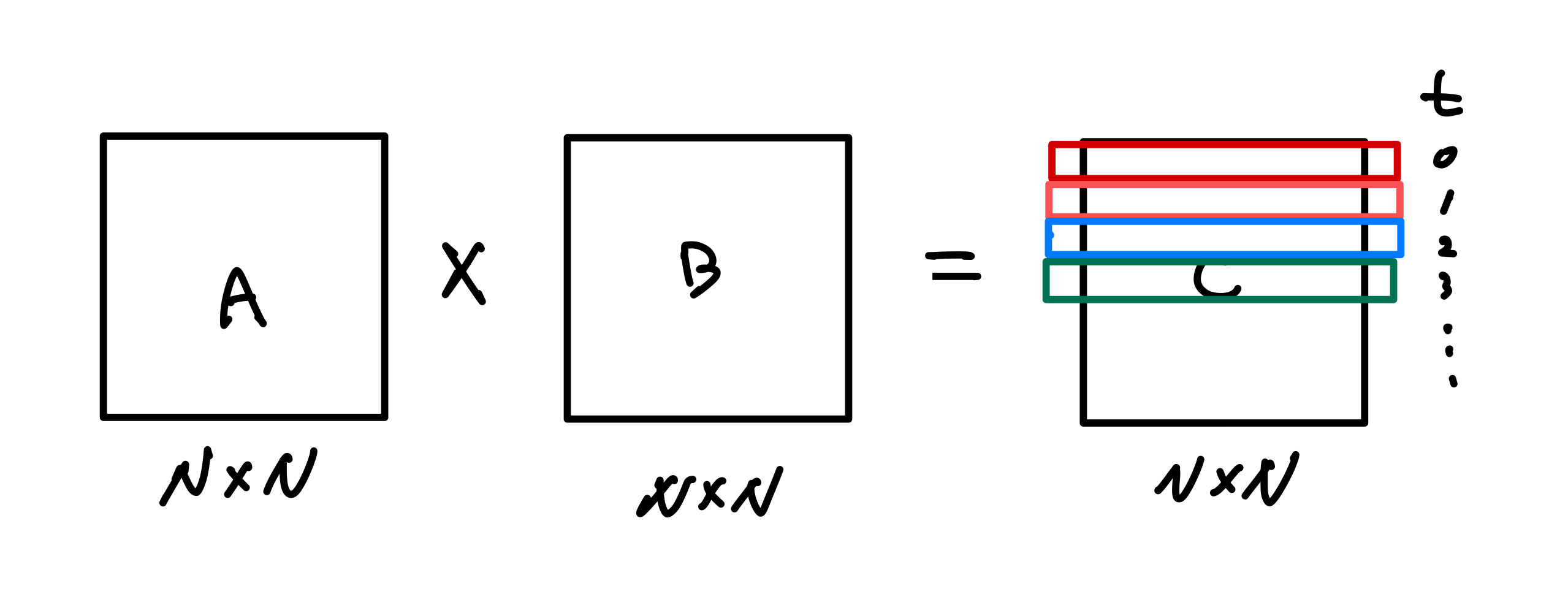
for i = tid to n step P // Row-wise block striping
    for j = 1 to n  
        for k = 1 to n
        	C(i, j) = C(i, j) + A(i, k) * B(k, j)

이렇게 Row-wise block striping을 통해 행렬의 곱셈을 하게 되면 각 쓰레드가 Write하는 부분들에 대해 Race condition도 존재하지 않으며 False sharing 문제도 없습니다.

그러면 행렬의 곱셈은 Row-wise block striping 방식으로 처리하는 것이 최선일까요?

정답은 아닙니다. 이 이유에 대해 이해하려면 먼저 Cache의 구조에 대해 이해해야 합니다.

3. Cache line

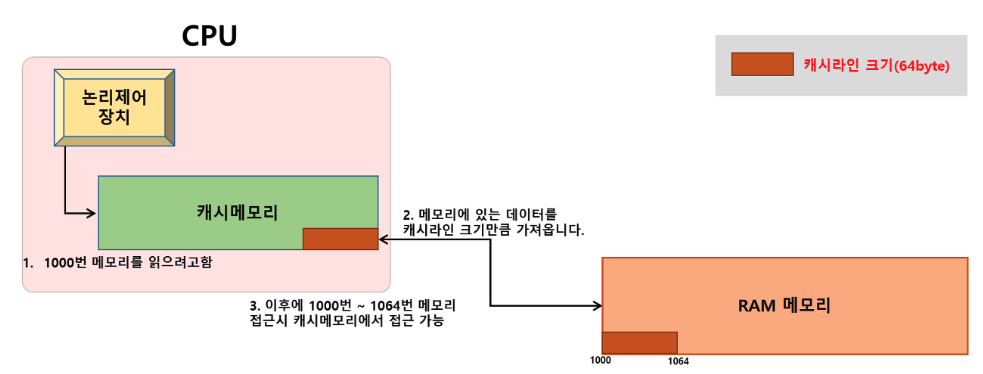
CPU에 가장 근접해있는 L1 Cache line의 크기는 약 64KB입니다. 이 때, 크기가 N * N인 행렬 A, B, C를 Cache에서 한 방에 읽어오기 위해서는 N = 64 정도가 최대 크기가 됩니다. 즉, N = 1,000과 같은 큰 행렬은 Cache line에서 한 번에 읽어올 수 없다는 것이죠. 그러면 결국 Cache miss가 날 때마다 다시 Cache에서 읽어오는 시간이 필요하게 됩니다.

뿐만 아니라, Cache line은 Row 방향 우선으로 데이터를 읽어오기 때문에 이전에 소개한 column-wise 방식으로 곱셈을 진행하게 되면 더 많은 Read 작업이 필요하게 됩니다.

정리하자면 A * B = C 행렬의 곱셈 연산을 하기 위해서는 최선의 경우(A, B, C 모두 Row 방향으로 읽는 경우)에도 아래와 같은 횟수만큼의 Cache line reads Operation이 필요하다는 것입니다.

A : N^2 / c reads (c = cache line size)
B : N^3 / c reads (c = cache line size)
C : N^2 / c reads + N^2 / c writes (c = cache line size)

그리고 문제는 여기에 있습니다. N = 1,000 이라고 하면 전체 연산을 위해 B 행렬은 1,000,000,000 / c 번이나 읽어와야 합니다.

그래서 이 문제를 해결하기 위해 Blocked Matrix Multiplication 방법이 등장합니다. 이 방법은 A, B, C 행렬을 작은 블록으로 쪼개서 Cache line의 사이즈에 맞추겠다는 아이디어에서 출발합니다.

4. Blocked Matrix Multiplication

아래와 같이 A, B, C 행렬을 작은 블록으로 쪼갭니다. 이 때 각 블록의 한 변의 길이를 b라고 하겠습니다.

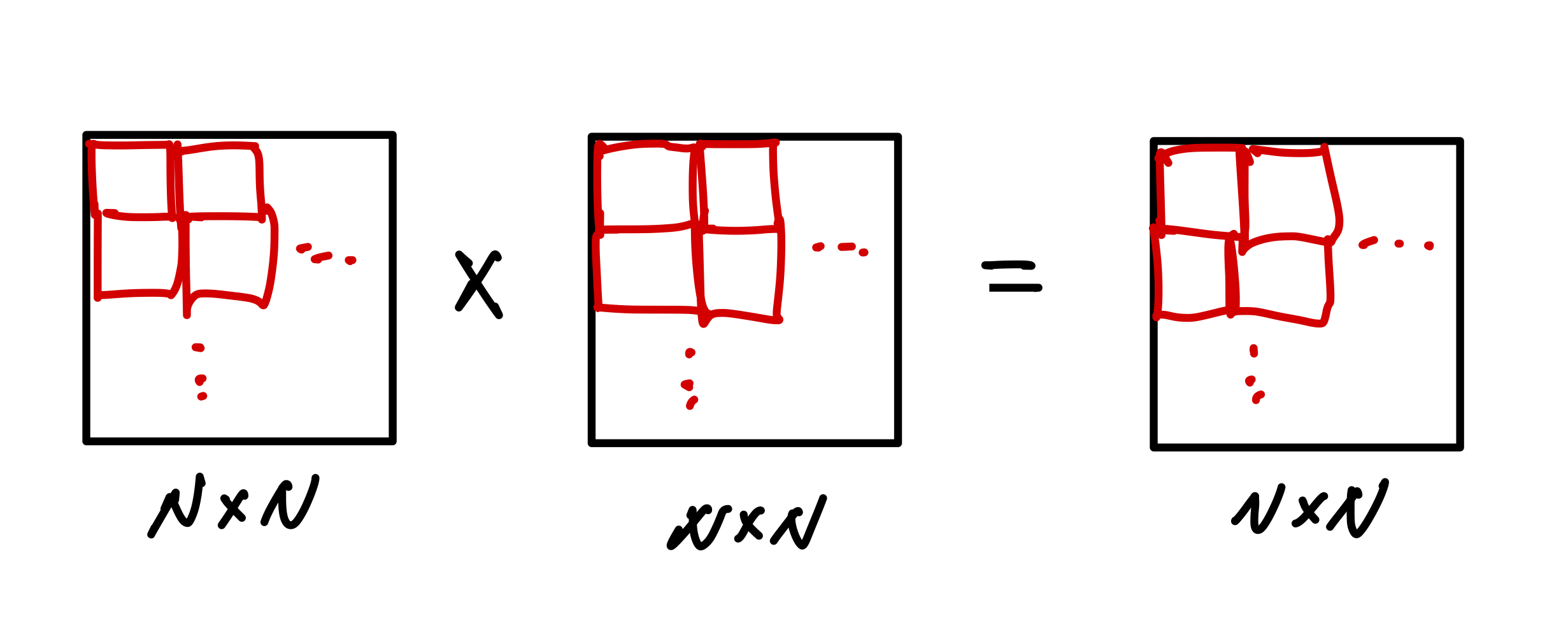
그러면 아래와 같은 코드로 행렬의 곱셈을 처리할 수 있습니다.

for i = 1 to n step b // Parallelize this part
    for j = 1 to n step b
        for k = 1 to n step b
            // multiply the matrix block
            for ii = 1 to b
                for jj = 1 to b
                    for kk = 1 to b
                        C(i, j) = C(i, j) + A(i, k) * B(k, j)

각 블록을 쓰레드에게 할당하게 되면 각 쓰레드는 Race Condition 없이 곱셈 연산을 할 수 있습니다.

그리고 Block 단위의 Multiplication의 효과를 보기 위해 이전의 방식과 비교를 해보겠습니다.

[Non-block]

A : N^2 / c reads (c = cache line size)
B : N^3 / c reads (c = cache line size)
C : N^2 / c reads + N^2 / c writes (c = cache line size)

[Block]

A : (N/b)^3 * (b^2 / c) reads (c = cache line size)
B : (N/b)^3 * (b^2 / c) reads (c = cache line size)
C : N^2 / c reads + N^2 / c writes (c = cache line size)

A는 Non-block에 비해 조금 늘어난 것 같지만 A, B를 통틀어서 보면

Non-block : N^2 / c + N^3 / c
Block : 2*N^3 / bc

위와 같으므로 b가 커질수록 block 방식에서 전체 작업이 b만큼으로 나누어져 더 성능이 개선되는 것을 알 수 있습니다.

5. 나가면서

이번 포스팅은 Matrix Multiplication을 어떻게 하면 더 효율적으로 처리할 수 있는지에 대해 공부했습니다. 특히 False sharing과 Cache line에 대한 이해를 하면서 단순히 Multithreading을 하는 것이 성능 개선의 전부가 아니라는 것을 알게 됐습니다.

Cache에 대한 이해가 조금 어려워서 잘못 설명한 부분이 있을 것 같습니다. 양해 부탁드립니다!

'CS > Multicore & GPU' 카테고리의 다른 글

[Multicore] 쓰레드의 Workload 관리와 Thread Pool에 대해 (0)	2022.03.17
[Multicore] Race Condition과 Locks (0)	2022.03.11

JSH 기술 블로그